

The following list gives you the difference in cents (100ths of a semitone) between equal temperament and just temperament for the notes of a major scale.
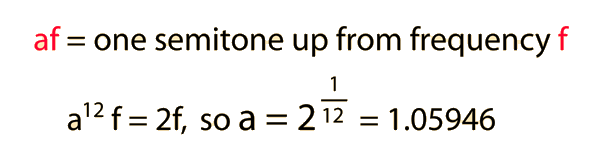
Now, when you compare the integer ratios with the frequencies obtained by equal temperament, you find that there are some differences. This is not an integer ratio - you can't get a pair of integers where you divide one into the other to get exactly 2 1/12.

The frequency ratio is 2 1/12 or about 1.059. But if you divide a 2:1 ratio into 12 equal ratios, you don't get integer ratios. By equal, that means equal in frequency ratio. True 12-tone equal temperament, which is what we generally mean by the phrase these days, works on the principle that an octave is divided into 12 exactly equal semitones. Bach wrote the Well-Tempered Clavier in order to demonstrate the possibilities of "well tempering" which was a form of nearly-equal temperament, showing that a single keyboard instrument could play reasonably in tune in all 12 major and minor keys. It took a while to catch on, but by the time of Mozart, it was universally used for the tuning of keyboard instruments. I'm not sure anybody knows who invented it, but Vincenzo Galilei (father of the astronomer Galileo Galilei) was one of the first recorded advocates of it. You can't instantaneously change the tuning of the a proportion of the strings whenever a piece modulates into another key! This mean that if a keyboard was tuned to just intonation in one key, it would sound distinctly odd if you play a piece in a key that is distant from it.Įnter equal temperament. But it is a bit of a problem for a keyboard instrument. Now, if you are singing, or playing a stringed instrument without frets, then this is not a problem, you can sing or play in just intonation for whichever key you happen to be in and you can make the necessary adjustments as you change key. So in G major, A is slightly sharper than in C major (assuming that G is tuned to be 3/2 relative to C).Īs you work your way through the various scales, you find that for every single scale, just intonation gives you different frequencies for some notes as compared to other scales which have those notes in common. In G major, the frequency ratio is 27/16, or 1.6875. In C major with just intonation, A has a ratio of 5/3, or 1.6667. G, B, C, D and E have precisely the same tuning. Now, compare these with the notes that are common to the C major scale. D 3/2 * 3/2 = 9/4 (halve the frequency to go down an octave = 9/8).So let's see what these ratios work out as when you multiply up. But the G itself has a frequency ratio to the original C. All these frequency ratios above apply, but relative to the G at the bottom of the scale. Now, if you look at a different key, G major for instance. The example of C major scale is as follows Each note is described in terms of its frequency ratio relative to the C at the bottom end of the scale. positions in the harmonic sequence relative to the key note). All the intervals of the major scale can be expressed in terms of these whole number ratios (i.e. For a true perfect 5th, the frequency ratio is 3/2. So here's another way of understanding how scales work, and why equal temperament is a compromise that makes notes sound equally "nearly" right in all keys.įirst of all, understand that for two notes an octave apart, the higher note is twice the frequency of the lower. And if you want to be a good musician, you have to have some kind of understanding of pitch and tuning. This isn't really quite about horn playing, but it quite clearly and obviously is about music - and if you want to be a good horn player then you must also be a good musician as well.


 0 kommentar(er)
0 kommentar(er)
